RSA

Explainations

RSA Encryption | MuirlandOracle | BlogMuirlandOracle | Blog

How does RSA work? | HackerNoonhackernoon

RSA is based on the mathematically difficult problem of working out the factors of a large number. It’s very quick to multiply two prime numbers together, say 17*23 = 391, but it’s quite difficult to work out what two prime numbers multiply together to make 14351 (113x127 for reference).

The details of the Decryption/Encryption pair:

1. Pick two prime numbers , I will pick 2 and 7 , lets call them p and q

P = 2 and Q = 7

2. Multiply P and Q , and that becomes the modulus

N = P * Q = 14

3. Make a list between 1 and N and remove the common factors or operate this operation (more easier):

( Q - 1 ) * ( P - 1) = L
(7 - 1 ) * ( 2 -1 ) = 6         # save this number , let’s call it “L”

4. Now we get to pick the encryption key , in the example was (5,14) , we know 14 is the modulus.

So for the encryption key there’s a few rules:

• it’s got to be between 1 and L

[2,3,4,5]

• Coprime (=no shared factors) with L (6) and the Modulus (14) , the answer is 5 , there’s no other possibility .

So there we came to a conclusion of why we picked (5,14)

5. The Decryption part , In the example we’ve picked (11,14) , again 14 is the modulus but where does 11 come from?? , from now on let’s call it D , let’s find out why D is 11:

D has to follow one rule and this is it:

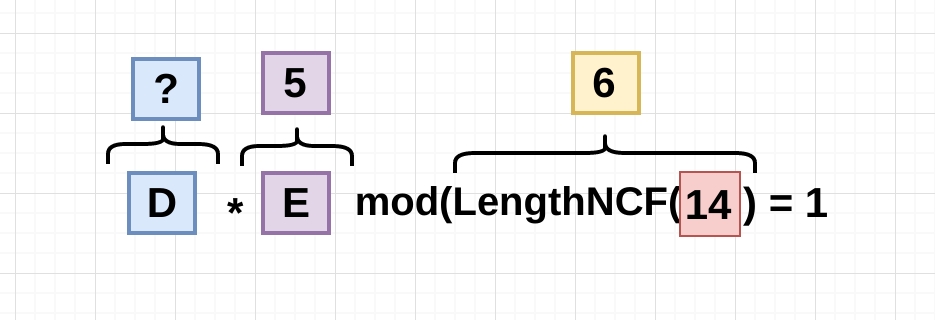
So the Decryptor(11) multiplied by the Encryptor(5) modulus the length of the non common factor with the modulus(14) has to be equals to 1.

D * E % LNCF(N) = 1
11 * 5 % 6 = 1

So we know if we multiply D * E and E is 5 , D will need to be a common factor of 5 , so:

So I’ve made a list of numbers from 1 to 50 and , filtered the ones that when multiplied by E and moduled by LNCF(N) are equals 1 , so let’s see if those can decrypt the message :) , Remember the encrypted message is “4”,and the decrypted message is “2” so the function should be something like:

4 ** D % 14 = 2 <---Decrypted message

So let’s do a little list comprehension to see if the rule works:

Great ! it worked , you see how applying the function to all the Decryption keys that follow the rule (D * E % LNCF(N) = 1) , decrypted the message successfully .